So You Want to Understand Bayes’ Theorem and/or Look at Photos of Cats

Back in 2010, researcher Daniel Daryl Bem at Cornell University supposedly proved that psychic precognition exists. He did a variety of tests on college students in which he reversed some common psychological tests and found that the students were able to predict something that had not yet happened. For example, he put pornographic photos behind one of two curtains. The students had to guess which curtain the photo was behind before seeing the answer and they were correct a statistically significant amount of the time. When statisticians use the term “statistically significant” they are typically referring to the p-value. If the study had a p-value cut-off of 5%, that would mean that if students were truly guessing randomly and did not have any psychic powers, they would still “pass” the test 5% of the time just by coincidence. So, supposing no bias, intentional or otherwise, answer the following question:
If Bem’s study on psychic powers had a p-value of 5%, what is the probability that the students were able to “pass” the test merely by coincidence rather than a true psychic ability?
My guess is that you probably answered this question with “Uh…Jamie, you already told us. There would be a 5% probability that the students passed the psychic test by coincidence.” Now, let me ask you a slightly different version of the same question:
Do you think it is more likely that the student’s in Bem’s study are truly psychic or that they just got really lucky?
Since you are currently reading Skepchick, you’re probably a skeptic and probably do not believe in psychic powers, so you likely answered this question by saying that you believe that the students in Bem’s study are not actually psychic. However, this means that you think it’s more likely that the students fell into the 1 in 20 tests that would pass by coincidence rather than that they are actually psychic. In other words, you believe there is an over 50% chance that the students are not psychic even though you previously said that according to the p-value there was only a 5% chance of the study being wrong. Regardless of what the p-value says, you know that the chance of there being real psychic powers is extremely unlikely based on the fact that there is no previous evidence of psychic powers. The problem with p-value is that it doesn’t take any past evidence into consideration.

So, if using a basic p-value for statistical significance of such an unlikely phenomena as psychic powers is flawed, then what can we use? Well, this is where Bayes’ Theorem comes in. You see, Bayes’ Theorem is a way of considering our prior knowledge in our calculation of probability. Using Bayes’ Theorem we can calculate the probability that the students in Bem’s study are really psychic or just got lucky in their guesses, while considering prior evidence as well as the new evidence. Lucky for us Bayes’ Theorem has a simple formula: 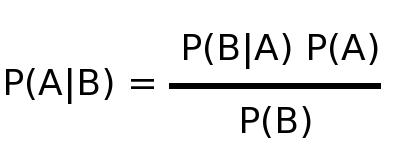 A formula is not very intuitive though, so let’s just ignore that for now because an equation is not needed for actually understanding Bayes’ Theorem. Instead of looking at a formula, let’s forget about Bem and his psychic students for a second and instead talk through the following scenario. One of our newest contributors here at Skepchick is Courtney Caldwell. The posts she’s done so far are pretty good, but what if she’s not who she says she is? What if she’s actually a spy! I mean, she says she a skeptic and a feminist and all that, but can we really know? She could have joined Skepchick just to spy on us for …. ummm….. whatever, look the point is that we just don’t know that she’s not a spy.
A formula is not very intuitive though, so let’s just ignore that for now because an equation is not needed for actually understanding Bayes’ Theorem. Instead of looking at a formula, let’s forget about Bem and his psychic students for a second and instead talk through the following scenario. One of our newest contributors here at Skepchick is Courtney Caldwell. The posts she’s done so far are pretty good, but what if she’s not who she says she is? What if she’s actually a spy! I mean, she says she a skeptic and a feminist and all that, but can we really know? She could have joined Skepchick just to spy on us for …. ummm….. whatever, look the point is that we just don’t know that she’s not a spy.
You see, it turns out that in this data that is totally 100% true and not something I’m just making up for purposes of this scenario, 15% of new writers at Skepchick turn out to be spies. To determine if Courtney is one of them, we’ll give her a polygraph test. Polygraphs are correct in determining lying versus truth-telling 80% of the time. Courtney says she is not a spy during the polygraph, but the polygraph tells us she is lying! So, what is the probability that Courtney is a real spy?

If polygraphs are right 80% of the time and the polygraph says Courtney is a spy, does that mean there’s an 80% chance she is an actual spy? How does the 15% probability of new Skepchicks being spies factor in? To answer this, let’s step back for a second and consider a theoretical scenario where we have 100 new Skepchicks. The following box represents 100 new Skepchicks. The blue skepchicks are the ones telling the truth while the purple ones are the secret spies (15% — but not to scale in the image just to make it clearer).
 We don’t know which people fall in the purple box or which in the blue, so we give them all a polygraph. They all claim they are not spies. The polygraph is correct 80% of the time, so out of our spies, 80% of them will be correctly identified as spies, while 20% will be misidentified as telling the truth even when they are not. In the following box, you can see that the 80% of the true spies that the polygraph labels as spies are represented in a red box and the 20% of the true spies that the polygraph has mislabeled as not spies are in the green box.
We don’t know which people fall in the purple box or which in the blue, so we give them all a polygraph. They all claim they are not spies. The polygraph is correct 80% of the time, so out of our spies, 80% of them will be correctly identified as spies, while 20% will be misidentified as telling the truth even when they are not. In the following box, you can see that the 80% of the true spies that the polygraph labels as spies are represented in a red box and the 20% of the true spies that the polygraph has mislabeled as not spies are in the green box. 
However, the spies aren’t the only ones that took the polygraph. All the new Skepchicks that were telling the truth about not being a spy also took the test. Because the polygraph is correct 80% of the time, 80% of the true Skepchicks were correctly labeled as not being spies, whereas 20% of them were misidentified as spies. The following box adds the polygraph results for the truth-tellers. Those in the green boxes were identified as telling the truth by the polygraph whereas those in the red boxes were identified as being lying liars.
However, we don’t know which Skepchicks are actual spies versus those that are telling the truth. All we know are their polygraph results. When considering the above box, all we can see is whether a person falls in the green box (pass polygraph) or red box (fail polygraph). For the sake of clarity, let’s label each of those boxes with a letter to make it easier to identify which box I am talking about at any given moment.
Let’s consider Courtney again. Courtney failed the polygraph, so what is the probability she is a real spy?
Considering the above boxes, you can see that Courtney falls only in one of the bottom two red boxes, boxes C or D, with her failed polygraph. We know that she is either a spy correctly identified by the polygraph (box C) or she is telling the truth but received a false positive on the test (box D). We don’t need to consider box A or B at all because we already know she failed the polygraph. Another way to phrase our question then would be: Given that we know Courtney failed the polygraph, what is the probability that she is in box C versus box D? Or, you can think of it as: C/(C+D) = probability Courtney is a spy!

In fact, we already have enough information to calculate the size of each box.
Box C is the probability that Courtney is a spy (15%) multiplied by the probability the polygraph is correct (80%): 15% * 80% = 12%
Box D is the probability that Courtney is not a spy (85%) multiplied by the probability that polygraph is wrong (20%): 85% * 20% = 17%
We can now easily get C/(C+D) –> 12%/(12%+17%) = 41.4% and…HOLY SHIT YOU GUYS WE JUST DERIVED THE FORMULA FOR BAYES’ THEOREM! Seriously, this complicated thing, which is the formula from before modified to incorporate our spy scenario:
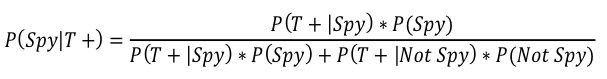 Just means that the probability that Courtney is a true spy given that she failed the polygraph is equal to the probability that the polygraph says she is a spy and she is a spy divided by the probability that the polygraph says Courtney is a spy regardless of whether she is or not. It’s just C/(C+D) in our box figure. In this version of the formula, I labeled each section to show how it relates to our box:
Just means that the probability that Courtney is a true spy given that she failed the polygraph is equal to the probability that the polygraph says she is a spy and she is a spy divided by the probability that the polygraph says Courtney is a spy regardless of whether she is or not. It’s just C/(C+D) in our box figure. In this version of the formula, I labeled each section to show how it relates to our box: 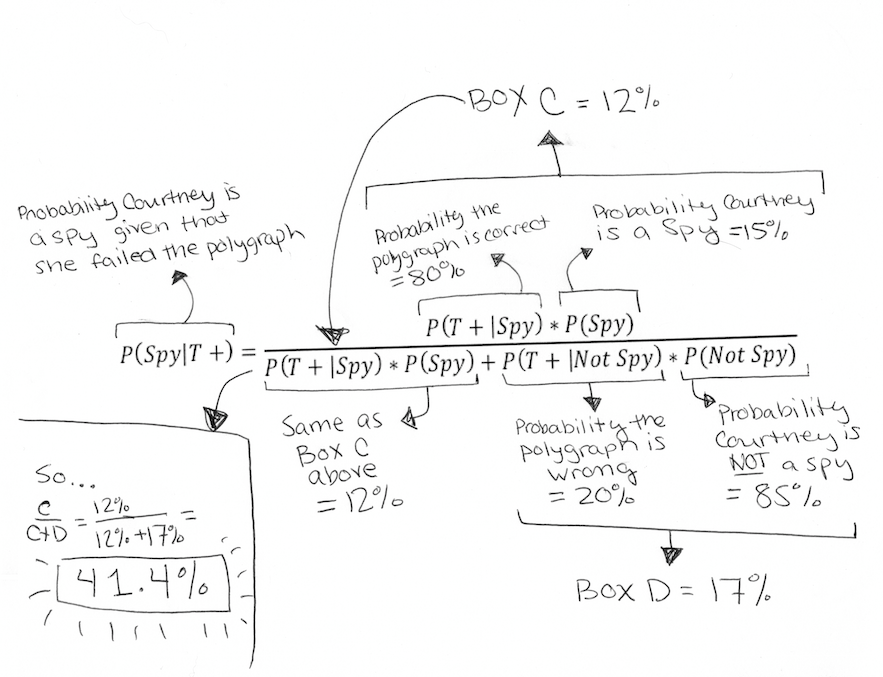 So, what does this mean exactly and how does it relate to Bem’s psychic research? The probability of Courtney being a spy pre-polygraph was 15%, but since we know she failed the polygraph the probability she was a spy went up to 41.4%. That means that even though the polygraph says that Courtney is a spy and the polygraph is 80% accurate, it is still more likely that Courtney is not a spy. In fact, there is a 58.6% chance that Courtney is not a spy! Yay!
So, what does this mean exactly and how does it relate to Bem’s psychic research? The probability of Courtney being a spy pre-polygraph was 15%, but since we know she failed the polygraph the probability she was a spy went up to 41.4%. That means that even though the polygraph says that Courtney is a spy and the polygraph is 80% accurate, it is still more likely that Courtney is not a spy. In fact, there is a 58.6% chance that Courtney is not a spy! Yay!
You can apply Bayes’ Theorem to any type of “test” where a true positive result is quite rare. For example, the fact that breast cancer is so rare is why if you get a positive result from a mammogram you still have a pretty big chance of not having breast cancer even if the test if fairly accurate. It’s also why the World Anti-Doping Association’s protocol requires athletes taking tests for doping to take a second different test if they get a positive result on the first one, rather than just trusting one test. Psychic abilities being real are almost infinitely more unlikely than breast cancer or doping so even though Bem’s research passed a 5% p-value threshold, it’s more likely that the test was wrong than not.
In fact, now that we know the formula for Bayes’ Theorem we can calculate it. Let’s say the chance of psychic powers being real was 1%, which is frankly a lot higher than the lack of evidence for such a phenomena would suggest. Let’s further say that Bem’s test has a 5% p-value, which is close to what he claims to have had on some of his tests. The p-value may suggest that there is a 95% chance that Bem’s students passed the test because they are truly psychic, but we can use Bayes’ Theorem to consider the previous evidence regarding psychic powers.
 Going back to our boxes, we want to calculate the values of C and D.
Going back to our boxes, we want to calculate the values of C and D.
Box C = The probability psychic powers are real (1%) multiplied by the probability Bem’s test is correct (95%) = 95% * 1% = 0.95%
Box D = The probability psychic powers are not real (99%) multiplied by the probability Bem’s test is wrong (5%) = 5% * 99% = 4.95%
Baye’s Theorem = C / (C+D) = 0.95%/(0.95%+4.95%) = 16.1%
In other words, even in extremely favorable conditions where the chance of psychic powers existing is 1% and Bem had a 5% p-value, the probability that psychic powers are real is still only a hair above 16%. The probability that psychic powers exist is much, much lower than 1% and none of this rules out the rather high probability of there being some sort of bias in the test protocols. It’s extremely likely that the positive result he got on his research is not a real one and in fact future researchers have been unable to replicate his results. Bem is certainly not the only researcher to “prove” a phenomena that does not actually exist. This is why many science-based researchers and skeptics have argued that Bayes’ Theorem should be used when considering whether results are statistically significant in research involving paranormal phenomena that are extremely unlikely to exist. Next time a study like Bem’s is released and you read articles asking why p-value was used instead of Bayes’ Theorem, you’ll know exactly what they are talking about.







Great post! Statistics are so interesting, and so confusing to me. Luckily cats pix are soothing to a confused mind. :-)
Wait… there was something other than cat pictures in that article? I think my brain has finally blocked out math due to all the trauma it has caused me. Look I know you don’t want to hear my sad story. It really is sad… look that’s not important what is that math and I have come to terms with each other we avoid each other at events we may both show up at, and I retained the right to do basic math you know like where money is involved or cooking but that’s it.
Oh and I am not psychic… and neither is anyone else…
okay one last thing I am reasonably sure cats will take over the planet someday opposable thumbs or not.
I’m not crazy
Jamie, I love this. When you explained this in person at SkepchickCON, something clicked and I finally understood Bayes’ Theorem. I’m so glad you were able to make it into a post. Wonderful job.
I’m glad you kept bugging me about it. This was originally a 3-post series on statistical significance but I had so much trouble with it and it went through 2 complete rewrites before I decided to just strip it of all but the Bayes stuff. Explaining math concepts in writing is so much more difficult than explaining it to someone in person.
There could’ve been so many more cat pictures … :-(
That is an excellent, pass-around-in-class-able rundown on Bayes Theorem.
But I want to know more about the 15% of new Skepchick bloggers that turn out to be spies. That’s not really true, is it?
For one thing, only a certain percentage of spies are ever uncovered. Maybe one in 10. So, that 15% is subject to further analysis…
I think I know where the 15% number came from. I think it’s the posterior estimate of the probability of being a spy after observing how suave, sophisticated, witty, and charming your typical Skepchick is. See, spies are known for being all of the above, P(suave | spy) = 1. Based on my totally great guessing skills, I estimate the number of spies employed by the CIA to be around 5,000, which is 0.16% of the U.S. population of 3.2 million people, so with a little rounding P(spy) = 0.0015. And the Skepchicks are clearly in the top 1% of suave, sophisticated, witty, and charming-ness, P(suave) = 0.01. Plugging into Bayes’ Theorem, the probability of being a spy given that you’re as suave, sophisticated, witty, and charming as a typical Skepchick is given by:
P(spy | suave) = P(suave | spy) * P(spy) / P(suave)
P(spy | suave) = 1 * .0015 / .01
P(spy | suave) = .15 = 15%
So just another example of the power of Bayes’ Theorem!
This is the best.
Love this post! It shows the math behind Carl Sagan’s (popularization of the) quote “Extraordinary claims require extraordinary evidence.”
If you’re making an extraordinary claim — something people think is very unlikely to start with, thus very low P(A) — you need very good evidence (way better than a 5% p-value) for P(A|B) to be convincing.
May i show this article my statistics class? Besides being a beautifully clear depiction of Bayes’ Theorem, its pretty damn funny, and i like to think my classmates will get a kick out of it.
Yes! That would be fantastic! I’m glad I succeeded in making Bayes understandable and fun. <3
This is fine as long as the researcher is genuinely open-minded about the truth. Since there is plenty of evidence from previous publications to suggest that Bem’s prior belief on precognition is very close to 100%, attempting to argue with him on this basis is comparable to an atheist arguing with a religious believer. And I suspect – given the number of depressing studies showing the extent of p-hacking and publication bias that seem to be appearing every week – that “doing whatever it takes to get my theory confirmed” instead of “attempting to find anything that might disprove my idea” may be more prevalent than we would like to think.
Great explanation! And really important not only for understanding pseudoscience but popular reporting of science more generally.
Some of my colleagues (in neuroscience) actually advocate for the abolition of the p-value in peer-reviewed work, arguing that it’s a number that’s so prone to misinterpretation, even by professional scientists who ostensibly know what it means, that it is as likely to mislead the reader as it is to accurately communicate the scientific results. But then, I’m at an unusually Bayesian school — this is probably real minority opinion in the neuroscience community at large, so you may wish to set your priors appropriately (har har I made a stats joke).
Excellent article, Jamie. You are my favorite blogger.
<3
Great description of Bayes’ theorem! However, you make a very common error in your discussion of p-values. You first state, correctly, that a p value of 5% means that if the student did not have psychic powers, they would pass the test 5% of the time. Unfortunately, you then restate this conclusion as “there would be a 5% probability that the student passed the psychic test by coincidence”. This is not true.
In Bayesian terms, it is true that P(passing test | no psychic powers) = 0.05. However, you are interested in P(no psychic powers | passing test). P(A|B) is not the same as P(B|A).
In plain terms, you want to know whether the students have psychic powers, knowing that the students passed the test. But all you know is that there is a 5% probability of passing the test, knowing that the students have no psychic powers.
What’s worse is that there is no good way to actually determine whether the students have psychic powers given any experimental results. You can’t use Bayes theorem, because first you would need to determine P(no psychic powers) – and of course, that’s part of the unknown.
This is a longstanding problem in statistics: scientists are forced to make with an expression of P(B|A), because P(A|B) is unknowable.
You’re actually restating the whole point of the article as though you were contradicting it, which makes me think you’ve misread it — another quick read might be warranted. Jamie put the incorrect interpretation “there would be a 5% probability that the student passed the psychic test by coincidence” in quotes, rhetorically attributed to the naive reader, precisely as the reasonable-seeming but actually-wrong interpretation which she then disproves, using the same reasoning from Bayes’ Theorem that you did.
Yes! That is… a restating of my entire post? The post was disproving the myth that if a test reaches statistical significance than it must be a true effect and vice versa. I apologize if it wasn’t clear. I did start out with some misconceptions so that I could later rip them apart.
I do disagree that P(no psychic powers) is unknowable. We know from a history of tests of psychic powers that they are very, very unlikely to exist (approaching 0%) because no other test of psychic powers has ever found evidence of them. Therefore we would need a lot of tests like Bem’s that all come up with positive results consistently in replications before we could really even think about considering it a real effect. As Carl Sagan said (and a commenter pointed out above) “extraordinary claims require extraordinary evidence.” That’s Bayes’ Theorem in a nutshell.
My totally informal understanding is that one way to interpret Bayes’ Theorem is as a way of representing how we should rationally change our beliefs on the basis of new information, though I’m no statistician, and I hope you’ll correct me if I’m wrong, Jamie.
That is, Skeptics who are familiar with tests of psychic powers might have the prior belief that P(psychic powers) is very, very small. People who are philosophically inclined toward a supernaturalist view of the universe might have a prior belief that P(psychic powers) is very large. People who haven’t ever put any thought into the issue might shrug and guess that P(psychic powers) = 50%. Then, Bem performs his experiment. No matter what your prior belief, you can apply Bayes’ rule to see how your beliefs should change to accommodate the new evidence.
Part of the problem for Skeptics is that if somone’s prior belief is that P(psychic powers) = 50%, then maybe their posterior belief, represented by P(psychic powers | Bem), should actually be to favor psychic powers. So for an ignorant but rational person, it could actually be totally reasonable to conclude that Bem’s experiment is convincing that psychic powers probably exist. The Skeptic’s job, then, is to show this person that P(psychic powers | Bem AND decades of failed paranormal research AND known physics, biology, and psychology) really is actually very small. A further problem, of course, is that most people (including Skeptics) aren’t actually rational in this way, with all the cognitive biases we all know about, including the bias to favor whatever information comes first. Living as we do in a society where experiments like Bem’s get more attention than negative results do, most people are probably more likely to encounter the individual small positive result before they encounter the huge mass of negative results (if they ever do).
In order to use Bayes’ theorem, as you note, you need to calculate Box C and Box D. Both depend on the probability that Bem’s are psychic, given the test results, i.e. P(students psychic | test results). In other words, you need the type I error rate. You seem to assume that this is equal to the p-value, i.e. 1 – P(test results | students psychic). And you start your calculations with this assumption:
“The p-value may suggest that there is a 95% chance that Bem’s students passed the test because they are truly psychic”.
“the probability Bem’s test is wrong (5%)”
Both of those statements are false. The p-value is *not* the type I error rate. In fact, determining the type I error rate usually requires making a bunch of extra assumptions.
The p-value only tells you the probability that you *would have* gotten the same results if you assumed the null hypothesis were true. Loosely, the p-value pertains to a hypothetical world, whereas the type I error rate pertains to the real world.
If I am just confusing you more, this explanation might help:
http://blog.minitab.com/blog/adventures-in-statistics/how-to-correctly-interpret-p-values
Hi StackExchangeUser1,
I’m not sure why you’re so interested in explaining “errors” which simply aren’t present in the original article. Once again, a more careful reading of what Jamie actually wrote should make it clear that she’s saying the same thing as you. You seem to have a strong… prior… that there must be an error in this article. Why is that?
You wrote:
But Jamie wrote:
(Emphasis mine.) The p-value cut-off (commonly denoted by alpha) is the false positive rate. By definition. Under standard frequentist hypothesis testing, you get to pick the false positive rate, which is kind of the whole point of having a p-value cut-off. So when you say:
I have no idea what you mean.
So yes, the p-value is not the false positive rate, but Jamie is pretty clearly not claiming that.
I do agree with you that out of context, Jamie’s sentence “The p-value may suggest that there is a 95% chance that Bem’s students passed the test because they are truly psychic” is a bit misleading. In context, I think it’s pretty clear what she meant (particularly given that the next word is literally “but”), but I suppose she might have been more clear by writing “may seem to suggest”. I’m not really sure what you’re going for by picking apart the phrasing so finely here — under the larger structure of the argument, it’s obvious that she’s making the exact same point that you are.
This is twice now that you’ve rather condescendingly explained an “error” that was actually just your own misreading of the article. If I am just confusing you more, this explanation might help: http://skepchick.org/2014/09/so-you-want-to-understand-bayes-theorem
Hi biogeo, I don’t mean to be condescending. I actually find this discussion quite interesting. But I still think you are wrong, I hope that’s ok.
You cannot use a p-value to calculate the probability that a single experiment is a false positive. Don’t take my word for it, though:
“Fisher was insistent that the significance level of a test had no ongoing sampling interpretation. With respect to the .05 level, for example, he emphasized that this does not indicate that the researcher “allows himself to be deceived once in every twenty experiments. The test of significance only tells him what to ignore, namely all experiments in which significant results are not obtained” (Fisher 1929, p. 191). For Fisher, the significance level provided a measure of evidence for the “objective” disbelief in the null hypothesis; it had no long-run frequentist characteristics.”(1)
It’s true that you could ignore Fisher and, following Neyman and Pearson, use alpha/beta to guide your experiments. In this case, though, you are following an a priori procedure to ensure that your false positive rate never exceeds alpha. You are not allowed to examine individual results to determine the level of evidence. Your experiments could have a 4.999% probability of error or a 0.0001% probability of error, you’ll never know. Again:
“Moreover, while Fisher claimed that his significance tests were applicable to single experiments (Johnstone 1987a; Kyburg 1974; Seidenfeld 1979), Neyman–Pearson hypothesis tests do not allow an inference to be made about the outcome of any specific hypothesis that the researcher happens to be investigating. The latter were quite specific about this: “We are inclined to think that as far as a particular hypothesis is concerned, no test based upon the theory of probability can by itself provide any valuable evidence of the truth or falsehood of that hypothesis (Neyman and Pearson 1933, pp. 290-291). But since scientists are in the business of gleaning evidence from individual studies, this limitation of Neyman–Pearson theory is severe.”(1)
To use Bayes’ theorem, you need to know the probability of error. I’m afraid neither the p-value approach (which does not give you the probability of error) nor the alpha approach (which only tells you its maximum value) will work.
Source:
(1) http://drsmorey.org/bibtex/upload/Hubbard:Bayarri:2003.pdf
Moderator(s), in retrospect I believe I linked to a source pdf which is not yet in the public domain. I’m sorry, I can’t seem to edit it. Please remove the link as necessary.
The citation follows:
The American Statistician. Volume 57, Issue 3, 2003. Confusion Over Measures of Evidence (p’s) Versus Errors (?’s) in Classical Statistical Testing. Raymond Hubbarda & M. J Bayarria
Sorry for taking a while to respond; I had some internet connection trouble last night.
I believe that you didn’t mean to be condescending. But, it comes across as condescending when you respond to an article that has the argument structure “You might think X, but actually Y, because Z” by saying “Well, you’re wrong about X, it’s actually Y, because Z.” Of course, a simple misreading means anyone can do that once, but after doing it twice… well, perhaps you’ll understand why that updates my posterior belief.
It’s totally okay that you think I’m wrong! I agree that this is an interesting topic for discussion, and exploring points of disagreement can be very informative. I’m having a bit of a hard time understanding what exactly you think I’m wrong about, though. You said, “You cannot use a p-value to calculate the probability that a single experiment is a false positive.” But, I never made any such claim. Nor would I make such a claim, because I think you’re absolutely right. In fact, as far as I can tell, no one here has made such a claim, so as far as I know we’re all in agreement here.
I do appreciate your bringing in some discussion of the Fisher and Neyman-Pearson interpretations of frequentist stats. I will admit that I always have a bit of trouble keeping Fisher’s interpretations straight, as I find them a bit abstruse, so it’s helpful to have it laid out here. I find the Neyman-Pearson interpretation much more straightforward. I will say that I find their epistemology which you quoted (“no test based upon the theory of probability can by itself provide any valuable evidence of the truth or falsehood of that hypothesis”), to be a philosophically sound position to hold, but so restrictive as to have little practical value, and I don’t think it’s an epistemological position we are required to take if we use frequentist statistics (if it were, statistics would be useless for science).
You wrote:
Again, in my opinion this is more of an epistemological issue rather than a statistical one per se. Certainly your position that P(B|A) cannot be known absolutely is consistent with the frequentist position, but in general Bayesians are quite comfortable using a less restrictive definition of “knowledge” and estimating P(B|A) according to some reasonable standard. At any rate, this strikes me as a rather technical point on which even professional statisticians disagree, and seems pretty far afield from Jamie’s article.
> in general Bayesians are quite comfortable using a less restrictive definition of “knowledge” and estimating P(B|A) according to some reasonable standard.
Yes, I think this is the crux of the issue! Bayesian interpretation is a wonderful way to express the added value of new knowledge, but it requires a consensus on what the new knowledge actually is.
For instance, you and I might have a hunch that Bem’s study has a false positive probability of ~5% (i.e. close to the upper limit imposed by alpha). But Bem could counter-argue that our intuition is wrong, and his intuition tells him that his work has only a ~1% false positive probability. There’s no easy way to resolve our differences. If he’s right, then the posterior probability of psychic powers existing would be 50%, not 16%. And note that I’m assuming that Bem is actually *skeptical* of psychics, and *shares* our 1% prior probability of the existence of psychic powers. The problem of priors is yet another issue, which needs no elaboration given your familiarity on the subject.
In short, to me Bayesian analysis seems best suited when dealing with non-controversial issues (e.g. using a diagnostic test for medical decision-making), but it runs into serious problems when used to back up arguments in an open debate.
You wrote:
This is a very interesting point. My expectation would be that good science demands that we take the most conservative position when interpreting our statistics. I.e., if I a priori say, “I will be applying a p-value cutoff of 0.05 when performing hypothesis tests in this study,” then I should also be committed to saying “I will accept the largest possible false positive rate estimate consistent with this cutoff, namely, 5%.” I think I can see why that isn’t a requirement based on the stats alone, but it seems like bad science to me to argue for a more generous false positive rate than what is imposed by alpha.
What’s funny is I think the Bayesians I know would make the exact opposite argument! I think they would say that frequentist analysis works fine when there’s general consensus on the methods and prior plausibility of a study’s possible outcomes, but that when there’s less general agreement about how we should proceed in interpreting a study, the Bayesian requirement that you make your assumptions very explicit aids in identifying points of disagreement.
No, that’s not how hypothesis testing works. I tracked down one of Bem’s papers, and in his pooled results he saw 2,790 hits out of 5,400 trials of “negative stimuli.” The Binomial test calculates the odds of that arising by chance as 0.7%.
His false positive probability is thus 0.7%. No more, no less, and no room for hunches. Neither of us can assert otherwise without providing additional evidence; I could find evidence he falsified some results, he could find evidence he recorded his trial data wrong, and actually had more hits, and so on.
So we’ve been walked through one example, but here’s where I always get stuck: what do we do with that result in the future? If my understanding is correct, the final result gets incorporated into the interpretation of the next test. So consider the two opposing scenarios: Jamie states her probability is 16.1% of psychic powers existing (using the 5% alpha) based on Bem’s 2010 study and prior evidence, HJ working with different assumptions (0.7% alpha) and get a result of 58.9% probability of psychic powers existing. So there’s some disagreement–that’s to be expected as new data frequently causes controversy.
We’ll settle it as all good scientists should by running another test. Let’s say Bem redoes his study exactly as he previously had. But this time the results are inconclusive, returning a nonsignificant pvalue = 0.30. How would this affect each person’s interpretation that psychic powers exist?
Sorry for the delay in response(s)!
alwayscurious: It’s to be expected that new data cause new controversy. But here, everyone agrees on the new data, and in principle everyone agrees on the aggregate meaning of all of the old data (summarized as the prior probability of psychics existing). Surely we should be able to reach a logical consensus in such a straightforward case?
biogeo: I’ve been thinking a while about your post, and I think I see a problem. You say that a conservative scientist would “accept the largest possible false positive rate estimate consistent with this cutoff, namely, 5%.” I would suggest that a conservative should only accept that FPR <= 5%. Isn't it more conservative to accept an inequality, with its maddening limitations, than force it into an identity? After all, science would look a lot different if we could actually solve for position using Heisenberg's inequality. Instead, we just accept the inequality, along with its epistemic implications.
Hj Hornbeck: I'm afraid you've fallen for the same trap (also reinforced by Santosh Manicka). There is a 0.7% probability of getting Bem's results if the students are not psychic. That's not the same as a 0.7% false positive rate (i.e. 0.7% probability that the students are not psychic).
Let me offer an imperfect analogy. Most medical researchers are familiar with the concepts of sensitivity, specificity, positive predictive value, and negative predictive value. Specificity, in particular, tells you what to expect *when you already know there is nothing to see*. Specificity can't be used to make useful predictions by itself. For that you need to combine it with an extra bit of information about the real world – disease prevalence – and derive the negative predictive value.
P-values are like specificity. They tell you what to expect when you already know there is nothing to see. Sadly, unlike specificity, it's very difficult to derive any predictive value from p-values. There is no good analogue for disease incidence in experimental science.
StackExchangeUser1 wrote “But here, everyone agrees on the new data, and in principle everyone agrees on the aggregate meaning of all of the old data (summarized as the prior probability of psychics existing).”
Sure in principle everyone should agree on a prior probability, but in practice they don’t. And there appears to be a debate about the exact nature of the probabilities in between. My question is this: Can a Bayensian approach eventually lead everyone to agree on a conclusion even if they have different starting points?
If the original prior probability firmly defines the final outcome, than Bayes seems rather weak: I firmly assume that no one will ever get a perfect or agreed upon prior–different people read different literature, accept different assumptions, etc. But if the original prior probability can eventually be overcome by a collection of evidence, than I can really appreciate its strength. Sit down with someone, run through the same gambit of research results and hammer out a narrowly defined posterior probability. But I’ve yet to find a multi-study example that demonstrates how that would happen. [And I’m not statistically literate enough to work through an effective one on my own]
StackExchangeUser1 wrote:
That’s an interesting point. I’m not particularly accustomed to seeing calculations involving false positive rates worked using inequalities, but it seems like there would be advantages to doing so. This actually fits with some (pretty informal) thinking I’ve been doing on the false negative rate regarding the reporting of negative results in science. It’s unfortunately very common (at least in my field) to read studies in which hypothesis tests yield p > .05, and the authors interpret this as “there is no effect”. Without having thought all that rigorously about it, it seems to me that it would typically be better to report an inequality on the effect size based on the false negative rate. I.e., something like “From our results we conclude that the effect of treatment X on observation Y is unlikely to be greater than E, if there is indeed any such effect.” I suspect it might be challenging to do this in a frequentist framework (though it should be possible), but it seems to my naive perspective a reasonably natural thing to do in a Bayesian framework. It has the advantage of turning a relatively weak negative statement (“we failed to reject the null hypothesis”) into a stronger positive statement (“the effect size is no greater than E”), which may have greater use in comparing similar studies and guiding future studies.
always curious:
You bet. Here’s a spreadsheet to help demonstrate that. Download a copy, tweak the variables, and prove it to yourself.
StackExchangeUser1:
I disagree. See my reply to Santosh Manicka for why.
Oops, my quotes actually came from a pre-publication version of that paper, and the last line of the second quote was omitted in the final version. The gist is the same, though.
Okay. So let me get this straight. You’ve got a 55/45 chance that it’s Bo Hopkins, and not Jerry Reed, on the Burt Reynold’s set. Then you’ve got a 33/33/33 probability split that it’s Dom DeLuise, Paul Prudhomme, or Luciano Pavarotti, in Dick Van Dyke’s kitchen behind the opera house. Burt Reynolds meets Dick Van Dyke for a drink. Aida is playing at the Met. Reed and Hopkins have aged equally poorly. There’s a Ford Gran Torino parked out back, big-block 7.0 429. Clint Eastwood is nowhere to be seen. But you hear that ooo-wooo-oo-wooo-oooooooo, from The Good The Bad & The Ugly.
Quick, who do you toss the keys to, Bo or Jerry?
Your cat is adorable and there’s no such thing as psychics because math. That’s what I got out of the post.
Actually, you might have just made a good argument for pre-cognition, as I’m shopping around an article on statistical analysis that invokes both the box metaphor and Bayes’ Theorem. Mind you, thinking of probabilities in terms of partitioning the space of all possibilities isn’t all that new or unheard of, so P(coincidence | two articles) > P(precog | two articles).
I agree with “StackExchangeUser1″‘s questioning of the assumption that “95% chance that Bem’s students passed the test because they are truly psychic”. The p-value of 5% only suggests that the probability of passing the test (getting some x or more answers to be correct) while being not-a-psychic is 5%. That is Pr(Pass | Not psychic) = 5%. This does not imply that Pr(Pass | Psychic) = 95%, because no assumption is being about what the “ground truth” is, that is what Pr(Psychic) and Pr(Not psychic) are.
To be precise, let me use the following notations:
P = Psychic; P’ = Not psychic; T = Pass test; T’ = Fail test
Pr(T) = Pr(T, P) + Pr(T, P’)
= Pr(P).Pr(T | P) + Pr(P’).Pr(T | P’)
We only know that Pr(T | P’) = 0.05
In order to calculate Pr(T | P), we ought to know Pr(T), Pr(P) and Pr(P’).
If and only if we (arbitrarily) assume these values are 50%, then it would turn out that:
Pr(T | P) = 1 – Pr(T | P’) = 1 – 0.05 = 0.95 or 95%.
From Bem’s experimental setup, specifically for experiment 2:
Bolding mine. Bem carefully set up the conditions so that if people were not precognitive, their success rate would be 50% in the long run. So we know that given an infinite number of trials, Pr( T | P’ ) = 0.5 and Pr( T’ | P’ ) = 0.5. We don’t know Pr( T | P ) or Pr( T’ | P ), but we know neither can equal 50%, and that random variation can cause Pr( T | P’ ) != 0.5 for small numbers of trials. The solution is obvious: run the experiment, calculate Pr( T ), then determine Pr( Pr(T) | P’ ).
I think that’s where you’re going wrong, by confusing Pr( T | P’ ) for Pr( Pr(T) | P’ ). We cannot dispute Pr(T), if the experiment was flawless, and as there are only two possibilities in the entire probability space (P and P’), it must follow that Pr( Pr(T) | P ) + Pr( Pr(T) | P’ ) = 1.
Ergo, if Pr( Pr(T) | P’ ) = 5%, Pr( Pr(T) | P ) = 95% by definition.
I have two responses to make:
1) By Pr(T) I meant the probability of *passing the test*. I haven’t read Bem’s paper, but I suspect that passing the test requires getting much more than 50% of the responses to be correct. If that is the case, then Pr(T) would be some value much less than 0.5. But I agree that if one randomly chooses their responses, they would be expected to get approximately 50% of them to be correct, assuming there is no other bias in the questions.
2) I am not sure what you mean by Pr(Pr(T)). Whatever it might be, it still should satisfy the following if it is random variable:
Pr(Pr(T)) = Pr(Pr(T), P) + Pr(Pr(T), P’)
= Pr(P).Pr(Pr(T) | P) + Pr(P’).Pr(Pr(T) | P’)
So, determining Pr(Pr(T) | P) still requires knowledge of Pr(P) and Pr(P’). Of course, it makes total sense to assume only P and P’ given the experimental conditions. But that says nothing about what proportions P and P’ are a priori.
1) There is no “pass” or “fail” for the test itself, because Bem had no idea how strong the precognition effect is. All he knows is that it cannot be equivalent to blind-chance guessing, as I said last comment. There were no questions, either, just photos; the methodology portion I quoted is for one experiment, but similar to the others in the paper.
2) What are the odds of determining the correct image? We can find that by doing multiple rounds, and dividing the total number of correct predictions (T) by the total number of predictions, which is denoted by Pr(T). If the person was guessing by blind chance, without precognition, then Pr(T) -> 50% as the number of trials reaches infinity. We’re not doing infinite trials, though, so we’ll get some number around 50%. So we need to take one more step, and calculate the odds, (Pr( …. )), of getting that successful test odds, (Pr(T)), assuming blind chance (Pr(T) | P), which translates to Pr( Pr(T) | P ).
I already explained why Pr( Pr(T) | P ) + Pr( Pr(T) | P’ ) = 1, and I hinted that Pr(Pr(T)) = 1 (“We cannot dispute Pr(T), if the experiment was flawless”).