Bad Chart Thursday: New Years Linked to Autism

Shocking news from the unironically named website The Mind Unleashed: “MIT Researcher’s New Warning: At Today’s Rate, Half Of All U.S. Children Will Be Autistic By 2025.”*
Autism: a fate worse than death for self-absorbed parents and people who benefit from demeaning those on the spectrum. It’s the go-to bogeyman for anyone who JUST KNOWS something is harmful but can’t prove it. In fact, I’m pretty sure that mushrooms, Ghosthunters, and my neighbor with the U.S. flag made out of Christmas lights** are all direct causes of autism. At the very least, there is a correlation.
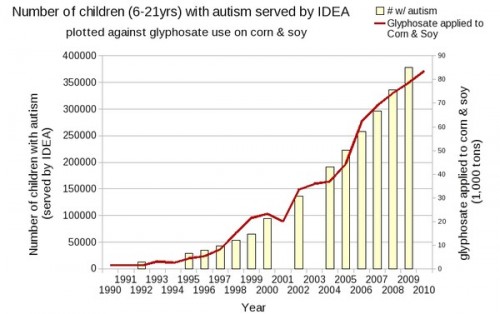
Kind of like the correlation shown in this chart between Roundup use and autism rates:
Now, despite the appeal to my inner conspiracy theorist, I can see a major issue with this chart and its interpretation.
Is it the use of two y-axes whose values can be adjusted to make the data fit as closely as you like?
Is it that the MIT researcher, Dr. Stephanie Seneff, is a computer scientist and AI researcher drawing comparisons outside her field of expertise?
Perhaps it’s the lack of context for the autism rates, such as the increasingly accurate diagnostic tools (in the past, people on the spectrum would not have been diagnosed as such and therefore wouldn’t be in the data), population growth, and so on.
Or maybe it’s simply the implication that this correlation has anything whatsoever to do with causation, that these two increases have anything to do with each other.
This list could go on, but what everyone seems to be missing is RIGHT IN FRONT OF OUR FACES: The increase in autism rates shown in this chart is clearly correlated with New Years.
Now, I don’t know if this means that New Year’s Eve or New Year’s Day causes autism, and if so, what mechanism exactly is at work. All I’m saying is that this correlation clearly deserves further investigation. Not that this will happen any time soon with Father Time and the calendar industry controlling Congress.
Big Calendar is freaking everywhere, people. You can’t deny that. So if you’re one of those people who fears autism and autistic people, don’t believe the Roundup smokescreen. Get rid of your calendars and probably your clocks (just to be safe). In fact, you might not want to leave the house in case you inadvertently measure time by the sun or night sky.
To everyone else, Happy New Year!
*Thanks to Kelly B. for sharing this article with us.
**Not making this up:





Bonus benefit of getting rid of your calendars and clocks: you won’t age!
Anthrosciguy,
LOL!
Getting rid of calenders would stop aging!
If time passes in the forest but there’s nothing around to measure it, do I still hate Mondays?
“Is it the use of two y-axes whose values can be adjusted to make the data fit as closely as you like?” Just elaborating on this point a bit, both overlaid graphs show approximately exponential growth. Lots of things show approximately exponential growth. E.g., Moore’s Law describes the change in processing power of computer chips as exponential growth. And, when rescaling the y-axis, all exponential growth curves can be made to look the same.* So I could construct a similar graph to show that the rise in autism follows a similar curve to the rise in computer processing power, and by similar reasoning argue that faster computer chips are causing autism. This point should be extremely obvious to any research scientist, so creating a graph like this one displays a willingness to use numbers to distort rather than inform. It is not inconceivable that chronic low doses of environmental toxins like pesticides could contribute to autism, but this is not evidence for that, and I’m not aware of any such evidence that is actually based in solid research rather than irresponsible speculation.
* Explanation: the general exponential growth formula is y = b * e^t, where y is the response variable, t is the independent variable (usually time), and b is a growth constant. Rescaling the y axis of any graph is equivalent to replacing y with c*y, where c is the amount by which to rescale. But this gives c*y = b * e^t, or y = (b/c) * e^t. Since b and c are both constants, this is the same as the original growth formula with a new value for b. So if I have two approximately exponentially growing phenomena with growth constants b1 and b2, I can always make them look the same by rescaling the graph of the second one by c such that c = b1/b2.
(BTW, sorry if there’s a double post on this — the site is really slow and from Cloudflare it looks like Skepchick might be getting DDOSed, so I’m not sure if my first post took.)