
Is it too late to write a post about The Force Awakens? Did I miss the zeitgeist? What if I offered you some science? It’s not too late to write about Star Wars and science, right?
I guess I should give the obligatory warning at this point that there will be minor TFA spoilers.
I’ve seen The Force Awakens three times. The first was just a blur of excitement. The second was blurrish. The third time, however, I managed to actually think about things and not let my mind get overpowered by lightsabers and space chases and BB-8. One thing in particular jumped out at me. In true Star Wars fashion, our plucky band of heroes must destroy a giant space weapon called Starkiller Base (also known throughout this post as “the base” or “SKB”) that can destroy entire systems of planets. It’s called Starkiller because it sucks up all the energy of a star and uses that energy to destroy planets.
Look, I didn’t say it was a realistic giant space weapon.
Anyway, this weapons basically devours a star. But, like, it’s also orbiting the star. It’s not eating some star a long way away. In the movie, we see it destroy the star it’s orbiting. What’s up with that?
Of all the weird and wild things that happen in the Star Wars universe, why did I sink my teeth into the orbit of Starkiller Base? I don’t know, man. Orbits have always seemed so delicate and choreographed to me. I like to see how I can mess that up. Luckily, I can do this without needing to actually destroy anything because this is 2016 and we can just use a computer. What follows is going to be a little math-y and a little computer-y, but stay with me.
I basically know nothing about orbital mechanics. (Due to family issues, I managed to miss that entire section in Theoretical Mechanics.) No matter! Newton’s Second Law and Law of Gravitation to the rescue.

Most people are probably at least passingly familiar with Newton’s Second Law of Motion: F = ma. But we also need to use Newton’s Law of Gravitation, because gravity is holding the base in orbit. (Newton is fine; no need to bring Einstein into this.) So to find out what the orbit of Starkiller Base looks like, all we need to do is equate the Second Law and the Law of Gravitation, move some stuff around, and solve a bunch of differential equations. But before that can happen, some assumptions:
1.) Star size: From the movie, I thought the star being destroyed in the final battle looked yellow, so I’m assuming that we’re dealing with a yellow star in the main sequence. Masses of yellow stars tend to fall in the 0.8 and 1.2 solar mass range. For this run I assumed the star is one solar mass.
2.) Mass of Starkiller Base: TFA, very helpfully, showed us the OT Death Star and Starkiller Base side-by-side. Assuming those sizes are to scale, the spacial dimensions of Starkiller Base can be calculated with reference to the Death Star. The only completed Death Star had a 120 km diameter. I estimated that that the size ratio of the Death Star to Starkiller base is 2:11 by finding a screen shot of the scene online and using graph paper to measure dimensions. I used the ratio to find that Starkiller Base has a radius of approximately 330 km.
From the movie, the landscape of Starkiller Base is covered in snow and evergreen trees and looked Earth-like. I assumed the density of the base to be similar to that of Earth: 5.5 g/cm3.Using that density and the volume of a sphere, I estimated the mass of Starkiller Base to be 8.31 x 1020 kg.
Look, I know there is a lot wrong with this assumption. People seem to be walking around like normal on the base, even though it’s not nearly the mass of Earth. However, if I took the base to have the mass required to simulate realistic Earth gravity with the base’s smaller radius, the base would have to be super dense. Like over 100 g/cm3. I don’t think trees are going to grow in that.
3.) Distance of Starkiller Base from the host star: Starkiller Base has a uniformly snowy terrain. As such, it’s clear that the base cannot be too close to its host star. I assumed the base was at least 2.28 x 108 km from its host star. So, Mars-ish distance.
4.) Orbital path: For simplicity, I assumed the Starkiller Base moved in a circular orbit.
Now that those assumptions are out of the way, we can get to actually figuring out what this orbit looks like. But, really, there are two orbits that need to be solved for, not just one. That’s because Starkiller Base and its host star are actually orbiting around their center of mass. Sure, in this case (as well as the Sun-Earth system) the center of mass happens to be inside the star, but the star is still undergoing an orbit. So that means there is a system of eight ordinary differential equations to solve.
Why so many equations? We can rearrange Newton’s Second Law and Law of Gravitation to solve to for acceleration, but that’s not really helpful. We want positions. We want x and y coordinates. Luckily, position, velocity, and acceleration are all related and we can get from one to another. Unfortunately, that means that for every coordinate we need to find, we have to solve two differential equations. Which is definitely why I’m using a computer. Specifically, I implemented a fourth order Runge-Kutta algorithm for this system of equations.
The 1 subscript corresponds to the position and velocity of Starkiller Base and the subscript 2 corresponds to the position and velocities of the star. The position coordinates are x and y, and the velocity is denoted by v.
While we don’t know very much about the base and the star, we can use the assumptions to figure out the period of their orbits. We just need to know the radius of the orbit and the mass of the orbiting bodies. To make things easy, let’s say that the star is at the origin and the base is at our assumed distance of 2.28 x 108 km on the x-axis, let’s call it R. This makes our initial position conditions easy. Now the coordinates of the base and star in the xy-plane are (R, 0) and (0, 0), respectively. And, because we are assuming a circular orbit and we can figure out what the orbital period is, we can figure out an initial velocity.
What we have here, then, is an initial value problem.
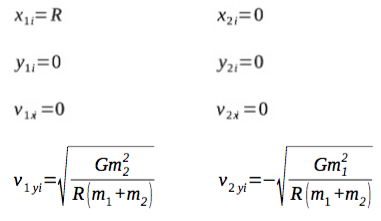 Where R is the distance of the base from the star, G is the gravitational constant, and m1 and m2 are the masses of the base and the star, respectively.
Where R is the distance of the base from the star, G is the gravitational constant, and m1 and m2 are the masses of the base and the star, respectively.
Remember, the whole point of this is to find out what the orbits of the base and the star do as the star loses mass. This was a three step process. First, I looked at the orbits of the star and planet without any mass loss by the star or mass accretion by the base. Those are just circles, as expected. Not terribly interesting. Next, I looked at the orbits of the the base as the star loses mass, but the base mass stays the same. I got this plot:
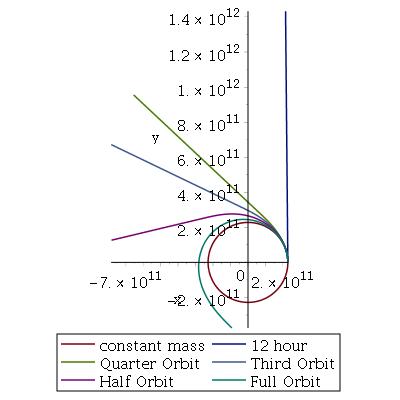 This plot shows the orbit of the base at various rates of mass decrease for a full SKB year with the x and y axes in meter. (OK, I know it’s not very neat. But the only plotting software I know how to use is Maple, which is also Satan’s favorite software.) It’s cool looking (which is why I’m sharing it, tbh), but not very illuminating. Its more interesting to zoom in and see what’s going on just during the time the star’s mass is decreasing.
This plot shows the orbit of the base at various rates of mass decrease for a full SKB year with the x and y axes in meter. (OK, I know it’s not very neat. But the only plotting software I know how to use is Maple, which is also Satan’s favorite software.) It’s cool looking (which is why I’m sharing it, tbh), but not very illuminating. Its more interesting to zoom in and see what’s going on just during the time the star’s mass is decreasing.
OK, what’s happening? These graphs represent the orbit of the base around a star of constant mass and the orbit of the base around a star that is losing mass until the star is gone. The red-ish-purple curve on these plots represent the constant mass case, and the blue line represents the base orbit as the star loses mass. The legend shows how long it takes for the star to lose it’s mass. One would expect that, as the star loses mass, its pull on the base would decrease and the star would gradually let go of its orbiting companion. That’s what we see. I had initially thought that the base would deviate much more from its original orbit before the star vanished. However, the more quickly the base depletes the star’s mass, the closer it is to it’s original orbit at the end.
But what if that’s not what happens in the movie? What if the base actually absorbs the mass of the star? What happens then?
It turns out, not much happens to the base. The orbit of the base that absorbs mass is the same as the base that doesn’t.
The orbit of the star, though? That’s a different story.
In the initial case, the star’s orbit changes as it loses mass. But check out what happens to the star’s orbit as its mass is transferred to Starkiller base.
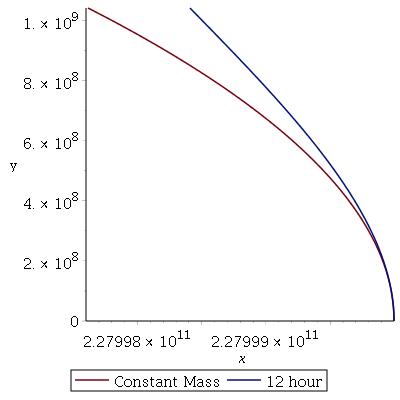
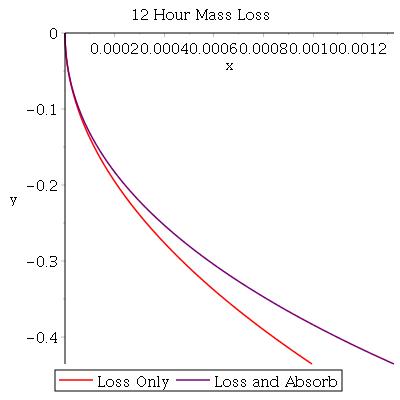
This plot shows what happens to the stars orbit if it takes 12 hours to transfer mass to the base. The red line represents mass loss only, and the purple line represents a situation in which the base takes on mass at the same rate.
Actually, neither of these paths are that different from the original circular orbit over 12 hours. In fact, when I tried to plot these over the star’s constant mass orbit, you couldn’t see these at all. And, really, this plot only represents 12 hours out of an entire SKB year, so what did I really expect? You can tell, though, that the ever-increasing mass of the base is tugging the star closer over time.
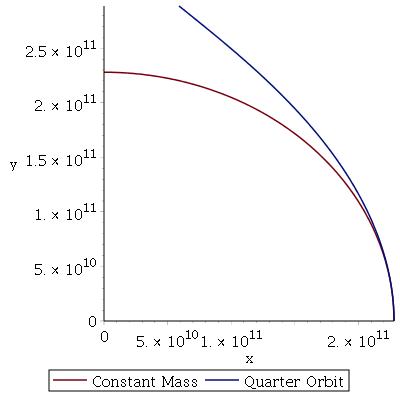
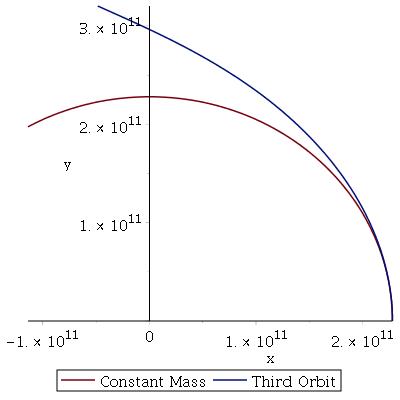
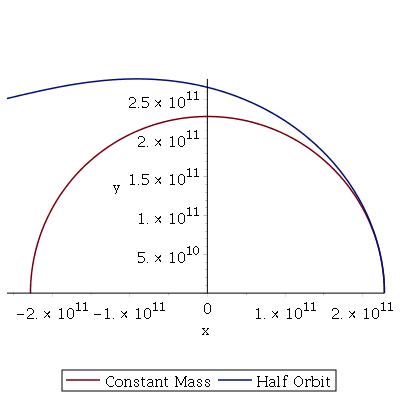
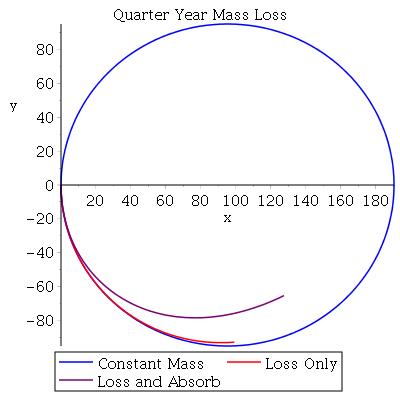
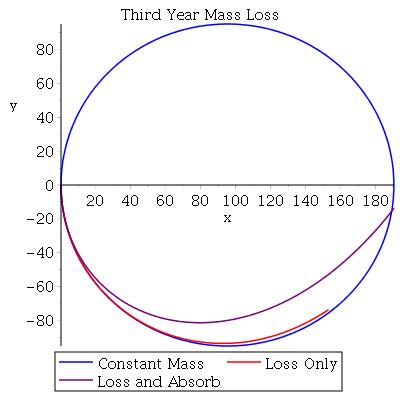
You can see this even more clearly in plots that assume a longer span of time.
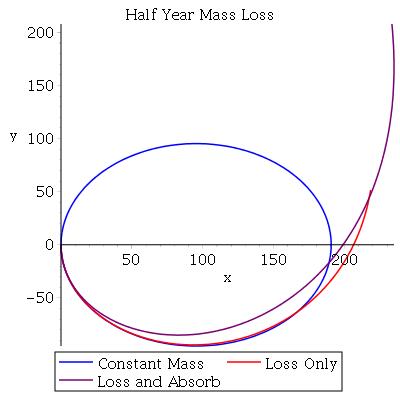 The blue on these plots show what the star’s orbit would look like after one SKB year. (That Half Year Mass Loss plot is just wonky; the orbit isn’t really elliptical.) The red and purple lines show the path the star takes until all of its mass is gone. The base in this situation is moving from it’s original position on the x-axis in a counter clockwise direction, and its increasing gravity is having an effect on the shrinking star.
The blue on these plots show what the star’s orbit would look like after one SKB year. (That Half Year Mass Loss plot is just wonky; the orbit isn’t really elliptical.) The red and purple lines show the path the star takes until all of its mass is gone. The base in this situation is moving from it’s original position on the x-axis in a counter clockwise direction, and its increasing gravity is having an effect on the shrinking star.
Neat, right? As the star gets lighter and the base gets more massive, the star is pulled in toward the base.
This project only has to do with the orbits of the base and the star it destroys. But that’s not all that’s weird with this situation. It’s been argued that by using the conservation of momentum and angular momentum we can show that Starkiller base would spin up so fast that everyone on the planet would fly off into space.
So the science of Starkiller Base isn’t perfect. That doesn’t matter. It’s wild fun, and I probably learned more about orbits from this project than I did from any class. Not bad.
*****************
Special shout out to my academic adviser who continued helping me with this project even though the first thing she said when I told her about it was, “But…it’s unphysical.” But what if, Dr. C? WHAT IF?


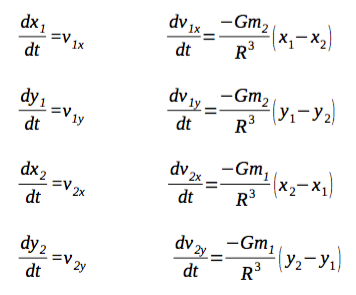




If you are interested in learning about orbital mechanics, I suggest playing Kerbal Space Program. The physics are simplified (e.g. single body, sphere of influence instead of n-body physics, spherical gravity wells), but by playing and watching the tutorials (kind of essential due to steep learning curve, I recommend Scott Manley’s youtube videos), you’ll get a good “learn by doing” idea of orbits, Hohmann transfers, and the Obarth effect.
The thing I noticed is that the actual laser behaves, like so much Star Wars light, in a way different than light actually behaves. At the very least, we know it travels faster than light, but not in hyperspace because Finn could see it.
When I saw it absorb the sun itself, I said “And now apparently the Empire runs on Joe Barton physics.”
But hey, rule of cool, amirite?